图的连通性

本分析参考自hihocoder

定义

割边：在连通图中，删除了连通图的某条边后，图不再连通。这样的边被称为割边，也叫做桥。

割点：在连通图中，删除了连通图的某个点以及与这个点相连的边后，图不再连通。这样的点被称为割点。

DFS搜索树：用DFS对图进行遍历时，按照遍历次序的不同，我们可以得到一棵DFS搜索树。

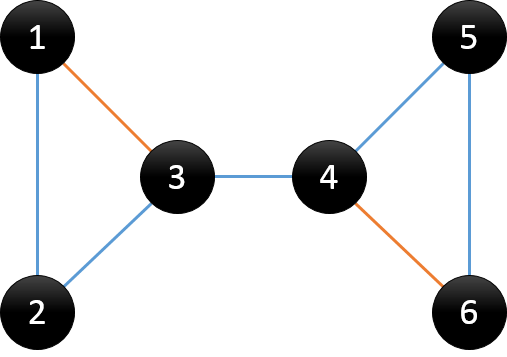
树边：在搜索树中的蓝色线所示，可理解为在DFS过程中访问未访问节点时所经过的边，也称为父子边

回边：在搜索树中的橙色线所示，可理解为在DFS过程中遇到已访问节点时所经过的边，也称为返祖边、后向边

有向图

强连通性

对于有向图上的2个点a,b，若存在一条从a到b的路径，也存在一条从b到a的路径，那么称a,b是强连通的。

对于有向图上的一个子图，若子图内任意点对(a,b)都满足强连通，则称该子图为强连通子图。

非强连通图有向图的极大强连通子图，称为强连通分量（SCC）。

更多参考：http://hihocoder.com/problemset/problem/1185

弱连通性

WCC: Weakly Connected Component

SCC：Strongly Connected Component

若存在一条从a到b的路径，或存在一条从b到a的路径，那么称a,b是弱连通（WCC）的。

无向图

边的双连通

对于一个无向图的子图，当删除其中任意一条边后，不改变图内点的连通性，这样的子图叫做边的双连通子图。而当子图的边数达到最大时，叫做边的双连通分量。

参考：http://hihocoder.com/problemset/problem/1184

点的双连通

对于一个无向图的子图，当删除其中任意一个点后，不改变图内点的连通性，这样的子图叫做点的双连通子图。而当子图的边数达到最大时，叫做点的双连通分量。

参考http://hihocoder.com/problemset/problem/1190

Tarjan算法

Tarjan算法经过改造，可以求： 1. 无向图的边双联通分量 2. 无向图的点双联通分量 3. 有向图的强连通分量（SCC）

而WCC可用迭代的方法求解。

复杂度： O(n+m) （n顶点数，m边数）

简单理解：

我们用dfn[u]记录节点u在DFS过程中被遍历到的次序号，low[u]记录节点u或u的子树通过非父子边追溯到最早的祖先节点（即DFS次序号最小），那么low[u]的计算过程如下：

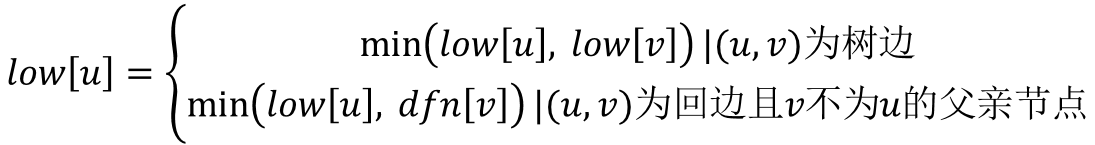
对于给的例子，其求出的dfn和low数组为：

id  1 2 3 4 5 6
dfn 1 2 3 4 5 6
low 1 1 1 4 4 4

可以发现，对于情况2，当(u,v)为树边且low[v]≥dfn[u]时，节点u才为割点。

而当(u,v)为树边且low[v]>dfn[u]时，表示v节点只能通过该边(u,v)与u连通，那么(u,v)即为割边。

遍历low，区分不同的值，即可知道哪些顶点在同一个连通分量中。

Tarjan算法的代码如下：

void dfs(int u) {
    //记录dfs遍历次序
    static int counter = 0; 

    //记录节点u的子树数
    int children = 0;

    ArcNode *p = graph[u].firstArc;
    visit[u] = 1;

    //初始化dfn与low
    dfn[u] = low[u] = ++counter;

    for(; p != NULL; p = p->next) {
        int v = p->adjvex;

        //节点v未被访问，则(u,v)为树边
        if(!visit[v]) {
            children++;
            parent[v] = u;
            dfs(v);

            low[u] = min(low[u], low[v]);

            //case (1)
            if(parent[u] == NIL && children > 1) {
                printf("articulation point: %d\n", u);
            }

            //case (2)
            if(parent[u] != NIL && low[v] >= dfn[u]) {
                printf("articulation point: %d\n", u);
            }

            //bridge
            if(low[v] > dfn[u]) {
                printf("bridge: %d %d\n", u, v);
            }
        }

        //节点v已访问，则(u,v)为回边
        else if(v != parent[u]) {
            low[u] = min(low[u], dfn[v]);
        }
    }
}

当然，上面的代码只是找到了割边，即“桥”，若要标记所有的连通分量，必须用一个栈来记录遍历的结点，每次访问一个新的结点，就push进去。 若到达桥，则pop出之前所有的结点，作为同一个连通分量。