Jimmy Blog
Welcome!
PageRank背后的数学
求解pagerank的值,实际上就是求解马尔科夫链的收敛值。
数学抽象
图的顶点值,能抽象成一个向量I。初始值为\(I_0\)。迭代过程就是I不断的与一个矩阵G相乘,最终I的值不变,则达到收敛。
Google Matrix
Google Matrix 就是上面所说的矩阵G,那么G如何获得呢?
矩阵A
A matrix element \(A{i,j}\) is filled with 1 if node j has a link to node i, and 0 otherwise; this is the adjacency matrix of links. 图中的边j->i,则\(A{i,j} = 1\)
矩阵S
A related matrix S corresponding to the transitions in a Markov chain of given network is constructed from A by dividing the elements of column "j" by a number of\(kj\) where \(kj\) is the total number of outgoing links from node j to all other nodes. The columns having zero matrix elements, corresponding to dangling nodes, are replaced by a constant value 1/N. Such a procedure adds a link from every sink, dangling state a to every other node.
S对应矩阵A中的元素,若A的某一列的元素非0,则S相应的列的元素的值,为A中列的对应元素除以当前列中非零元素的个数;若A的某列都为0,则S对应的列的值为\(1/N\),其中N为矩阵的维度。例如:
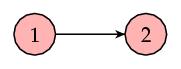 则S为:
则S为: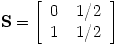 ;
;
矩阵G
Then the final Google matrix G can be expressed via S as:
$$G = \alpha S + (1-a) \frac{1}{N}$$
By the construction the sum of all non-negative elements inside each matrix column is equal to unity. The numerical coefficient \alpha is known as a damping factor.
Usually S is a sparse matrix and for modern directed networks it has only about ten nonzero elements in a line or column, thus only about 10N multiplications are needed to multiply a vector by matrix G.
幂法(power iteration)求解
之前其实就解释过了,简单来说,就是I不断的与一个矩阵G相乘,最终I的值不变,则达到收敛。
幂乘法可取吗?
I经过多次与G相乘最终收敛,根据结合律,可以写成 \( I = G^n{I_0} \)。 实际上是G自己的n次方收敛了。采用“幂乘法”先把收敛的\(G^n\) 求出来,看似矩阵相乘的次数变少了,只需要G平方\(log(n) + 1 \)次,实际上这是错误的。G每次平方,复杂度都是向量I乘以G的n倍,n是G的维度。迭代收敛次数往往是小于n的,所以,直接用向量乘矩阵会快一些。
例如,G的维度是1000,I乘上G,迭代500次即可收敛(即 \( G^{500}\)收敛),而计算G的n次方收敛需要7次,才能达到\( G^{512}\),收敛,而一次G的平方耗费的时间是I与G相乘的1000倍,复杂度远远超过预期。所以,“幂乘法”是不可取的。